Mathematics tutors
Our IB Maths Tutors say that Trigonometry is a very important and interesting branch of Maths
Trigonometry is one of the branches of Mathematics that fascinates Mathematicians. It tells about the relationships between the angles and sides of a triangle. Word trigonometry was started from the Greek word, where,
‘TRI‘ = Three
‘GON‘= sides and the ‘METRON’ = to measure. It’s an ancient and probably most widely applicable branch in Mathematics.
Parts of Trigonometry-
For basic learning, I am dividing trigonometry in two-part:-
1 Trigonometry based on right triangles
1 Trigonometry based on non-right triangles.
In this post, I will only discuss Trigonometry based on right triangles.
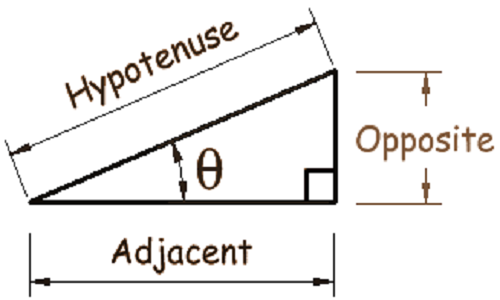
In a right triangle, there are three sides hypotenuse (the longest side), adjacent side(base) and the opposite side(perpendicular).
Pythagoras theorem
If we know any two sides of the right triangle, we can find the third side by using Pythagoras theorem:-
P²+B²=H²
In a right triangle, the ratios of sides can be written in many ways like P/H, B/H, P/B, H/P, H/B, B/P. each ratio is called a trigonometric ratio and these are represented by Latin words Sin, Cos, Tan, Cosec, Sec and Cot.
In a right triangle
Sin =P/H, Cos =B/H, Tan= P/B, Cosec= H/P, Sec =H/B, Cot= B/P,
Mathematics tutors use these three concepts to solve trigonometric problems
Concept-1
In a trigonometric problem, If we are given a trigonometric ratio or asked about it, we will first find all three sides of the triangle
Using the above concept and above formulas, we can solve the first type of trigonometric problems
Sample Problems
Example-1 If sin θ = 8/17, find other trigonometric ratios of θ.
Ans-
Let us draw a ∆ OMP in which ∠M = 90° 
Then sin θ = MP/OP = 8/17.
Let MP = 8k and OP = 17k, where k is positive.
By Pythagoras’ theorem, we get
OP2 = OM2 + MP2
⇒ OM2 = OP2 – MP2
⇒ OM2 = [(17k)2 – (8k)2]
⇒ OM2 = [289k2 – 64k2]
⇒ OM2 = 225k2
⇒ OM = √(225k2)
⇒ OM = 15k
Therefore, sin θ = MP/OP = 8k/17k = 8/17
cos θ = OM/OP = 15k/17k = 15/17
tan θ = Sin θ/Cos θ = (8/17 × 17/15) = 8/15
csc θ = 1/sin θ = 17/8
sec θ = 1/cos θ = 17/15 and
cot θ = 1/tan θ = 15/8.
Example-2 If cos θ = 3/5, find the value of (5cosec θ – 4 tan θ)/(sec θ + cot θ)
Answer-
Let us draw an ∆ ABC in which ∠B = 90°. 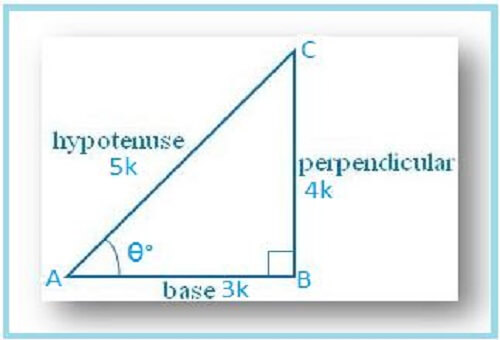
Let ∠A = θ°
Then cos θ = AB/AC = 3/5.
Let AB = 3k and AC = 5k, where k is positive.
By Pythagoras’ theorem, we get
AC2 = AB2 + BC2
⇒ BC2 = AC2 – AB2
⇒ BC2 = [(5k)2 – (3k)2]
⇒ BC2 = [25k2 – 9k2]
⇒ BC2 = 16k2
⇒ BC = √(16k2)
⇒ BC = 4k
Therefore, sec θ = 1/cos θ = 5/3
tan θ = BC/AB =4k/3k = 4/3
cot θ = 1/tan θ = 3/4 and
csc θ = AC/BC = 5k/4k = 5/4
Now (5cosec θ -4 tan θ)/(sec θ + cot θ)
= (5 × 5/4 – 4 × 4/3)/(5/3 + 3/4)
= (25/4 -16/3)/(5/3 +3/4)
= 11/12 × 12/29
= 11/29
In next post of Mathematics tutors series, we will discuss the remaining two concepts of non-right triangle trigonometry
To get a better understanding of the concept you should check all my posts of Mathematics tutors series. you can check them by clicking on the links given below
First post- concept one (current post)
Second post- concept two(current post)
Third post -Concept three
Fourth post -Concept four