Maths tutors
IB Maths Tutors gives great importance to Trigonometry.
Trigonometry is a branch of Mathematics that fascinates me as a teacher very much. It states the relationships between the sides of a right triangle and its angles. Word trigonometry was first used by the Greeks where
‘TRI‘ is Three, ‘GON‘ is sides and the ‘METRON’ is to measure. It’s an ancient and probably most widely utilized branch of Mathematics. For basic learning,
Maths Tutor divide trigonometry into two parts:-
1.Right triangles based Trigonometry
2. and the one based on non-right triangles.
Here, we are discussing trigonometry based on right triangles only.
In the third article of this series, we will discuss problems based on complementary angles
In the third article of this series, we will discuss problems based on complementary angles
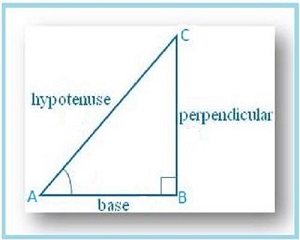
In this right triangle Sin A=BC/AC & Cos C=BC/AC clearly: Sin A=Cos C In the given triangle A+C=90° so we can write C=(90°-A). This gives us freedom to write Sin A=Cos (90°-A) similarly we can write these relationships
tan A=Cot (90°-A)
CotA=tan (90°-A)
SecA=Cosec (90°-A)
Cosec A=Sec (90°-A)
Sin A=Cos (90°-A)
Cos A= Sin (90°-A)
These formulas give us the freedom to solve trigonometric problems based on complementary angles. Maths Tutor use the following concept to solve complementary angle problems
Concept-3
In a trigonometric problem, If we are given two angles that are complementary to each other, we will change only one angle out of the given two angles. We should keep the second angle unchanged.
Example 1: Find the value of cos 56° / sin 34°
Solution: 56°+34°=90° so given angles are complementary. In the case of complementary angles, we should change only one angle. here we are changing at 34°
cos 56° = cos (90° – 56°) = sin 34°
cos 56° / sin 34° = sin 34° / sin 34° = 1
Hence the value of cos 56° / sin 34° is 1.
Example 2: Find the value of (cos 65° sin 18° cos 58°) / (cos 72° sin 25° sin 32°)
Solution :
65° and 25°
18° and 72°
32° and 58° all are pairs of
cos 65° = cos (90° – 25°) = sin 25°
sin 18° = sin (90° – 72°) = cos 72°
cos 58° = cos (90° – 32°) = sin 32°
(cos 65° sin 18° cos 58°) / (cos 72° sin 25° sin 32°) is
= (sin 25° cos 72° sin 32°) / (cos 72° sin 25° sin 32°)
= 1
Hence the value of the given trigonometric expression is 1.
Example3: I the value of sin 3A = cos (A – 26°), where 3A is an acute angle, then calculate A.
Solution: We are given that sin 3A = cos (A – 26°)
cos (90° – 3A) = cos (A – 26°)
90° – 3A = A – 26°
To get a better understanding of the concept you should check all my posts of Mathematics tutors series. you can check them by clicking on the links given below
First post- concept one
Second post- concept two
Third post -Concept three (current post)
Fourth post -Concept four
