For IB Maths Tutors both HL and SL, functions are one of the most important areas because they lie at the heart of much of mathematical analysis.here I am discussing domain and range of a function
Domain of a Function
Suppose I say that f is a real function.This means that for real input, the output should be real. For example
F(x)=√x
if F is real, then x can only take non-negative values because only then the output will be real. Set of all real values of R is called domain
“Domain is the set of all possible inputs for which the output is real ”
In some cases, x is defined explicitly. for example,
y=f(x)
=x²; 1<x>2 here domain is defined explicitly as (1,2)
If no domain is mentioned explicitly, the domain will be assumed to be such that “F” produces real output
These are a few examples
- y=f(x)=√x
Domain D= x≥0
2) f(x)=√x
Domain D= 2∠x≤3 or x∈(2,3)
3) y=1∕x then domain will be any real number excluding zero
Domain D=ℝ-{0}
4) y=logx then the domain will be any positive integer because logs are only defined for positive real numbers
D=x≥1
Range of a function- It is simply the set of possible outputs for a defined domain.
Range depends upon domain
Examples:
1) y=x²
Domain x=ℝ
Range y≥0
2) y=√x
Domain x≥0
Range y≥0
3) y=√x 2∠x≤3
Domain x=(2,3)
Range y=(√2,√3)
Question asked in IB Mathematics are usually more complex than above examples
To have a graphical picture in mind, consider this image
When plotted on a graph, the independent variable (x) is plotted on the horizontal axis while the dependent variable (y) is plotted on vertical axis
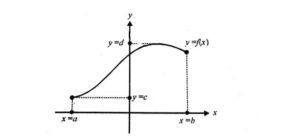
Suppose y depends on x as shown in above figure. You can easily tell the domain and range of the function just by looking at the above figure.
Domain D=a≤x≤b or
D=[a,b]
look along the y axis and we see that the graph only varies only between certain values of y
so Range R=c≤x≤d or
R=[c,d]
To summarise, for domain look along x-axis, for range look along y-axis
It’s practice time now :)-
Try these questions and find domain and range of a function.pdf
In my next article on IB Mathematics, I will discuss various types of functions
