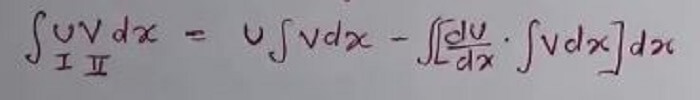Indefinite Integration
After a long series on differentiation and ‘Application of derivatives’, Online IB Tutors will now discuss Indefinite Integration. It consists of two different words indefinite and integration by IB Maths Tutors .
First of all, we shall learn about Integration.
Integration is the reverse process of differentiation so we can also call it as antiderivative. There is one more name for it, that is Primitive.
If f & g are functions of x such that g'(x) = f(x) then the function g is called a Primitive Or Antiderivative Or Integral of f(x) w.r.t. x and is written symbolically as:-
If
then here c is just an arbitrary constant. Value of c is not definite that’s why we call it Indefinite Integration.
Techniques Of Integration-:
There are a few important techniques used to solve problems based on an integration
(i) Substitution or Change of Independent Variable- If the derivative of a function is given in the question, then we should use the method of substitution to integrate that question.
Example-1 Find integration of this problem
Ans- Here derivative of is 2x that is given in the question so we can substitute
by some other variable. let
=t
If we differentiate both sides
2x.dx=dt
so =
+c
(ii) Integration by part- If we are given the product of two functions such that we are not able to use the method of substitution to integrate it, then we use Integration by parts. Suppose u and v are two functions then-
Note-: While using integration by parts, choose u & v such that we can easily apply above formula and reduce the given function from a product of two functions into a function that can be easily integrated. For this, we choose u in the order of ILATE. Here
I inverse function
L Logarithmic Functions
A Algebraic Functions
T Trigonometric functions
E Exponential function
Some people use the above formula in a different way
they choose F(x) in this order: LIPET
logs, Inverse, Polynomial, exponential, trigonometric
(iii) Integration by Partial Fractions- Partial fraction is a long and different topic. We use it in integration to simplify some complex fraction. I have attached a whole module on this topic at the end of the post
(iv) When the Power of Numerator is More Than the Power of Denominator- In this case, we first divide the numerator by denominator to make it a pure fraction, then we can use the partial fraction to simplify and integrate it.
Integrals Of Some Special Type-
Here we have some special types of functions and tricks to integrate them.
(i) or
in these cases, we let f(x)=t
(ii) ,
in all these cases we convert
() into a perfect square
(iii) ,
in these cases we Express:-
px + q = A (differential co-efficient of denominator) + B
(iv)
(v)
(vi)
(vii)
in this case, we take
common and put
= t
(ix)
in this case, we take
common and put
= t If we
If we take care of all these rules properly, then we can solve all the problems of definite integration.
Here I am attaching a full module on Integration by Partial fraction
A pdf containing almost all formulas of indefinite integration
A pdf of a few questions based on the integration
In the next post, I shall discuss Definite integration
Hire the best IB Maths Tutors and IB Tutors in Delhi and get the best grades