polar form of complex numbers,,Euler and de-moiver theorem

Polar Form of complex numbers

In the previous post, Our IB Maths Tutors discussed the basics of complex numbers. This is the second and final post on complex numbers. Here we shall discuss, polar form of complex numbers
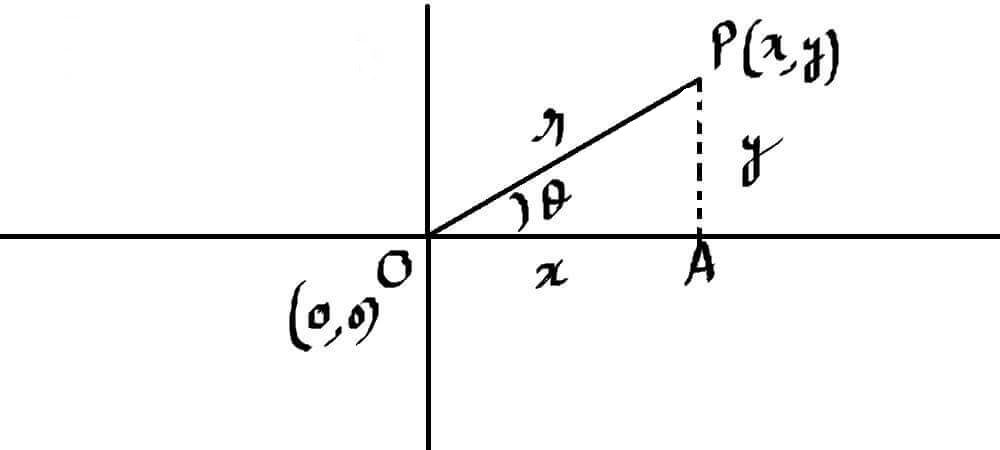
We consider complex numbers like vectors and every vector must have some magnitude and a certain direction. If we write a complex number in form of a point in the Cartesian plane/ordered a pair like x+iy=(x,y) then the distance of this point from the origin (0,0) is equal to the magnitude of our complex number while the angle it’s making with x-axis will show it’s direction.

In the above right triangle, using Pythagoras theorem

${r^2} = {x^2} + {y^2}$ so the magnitude of the complex number/vector

$\left| z \right| = r$

$\left| z \right| = \sqrt {{x^2} + {y^2}}$ and in the same triangle, $\tan \theta = \frac{y}{x}$ $Sin\theta = \frac{y}{r}$ $Cos\theta = \frac{x}{r}$

and $\theta = {\tan ^{ - 1}}\frac{y}{x}$ here $\theta$ represents the direction of complex number/vector. This is called the argument of a complex number

$z = r(\frac{z}{r})$

$= r(\frac{{x + iy}}{r})$

$= r(\frac{x}{r} + i.\frac{y}{r})$

$z = r\left( {Cos\theta + iSin\theta } \right)$ this is called the polar form of complex numbers z. Magnitude $\left| z \right|$ and argument $\theta$ can be calculated using above-mentioned formulas. So this way we find the polar form of the complex number

VERY IMPORTANT NOTE:- As we have already discussed, a complex number is like a point that can lie in any quadrant of the Cartesian plane. We should always consider the quadrant of the point while calculating argument and finding the polar form of complex numbers

Example:- Find the polar form of complex numbers given below

Solution

(a) Let’s find out r

We can see, ordered-pair of the given complex number is (-1, $\sqrt 3$ ). It should be lying in the second quadrant so the argument must satisfy

Tan is negative in both second and fourth quadrants but we shall only consider second quadrant value because our complex number is lying there.

therefore the polar form complex number is-

If we are after all the possible value of the argument then:

Exponential Form of a Complex Number-

After rectangular form and polar form of complex numbers, this is the third form of a complex number. To find it, we take help from Euler’s Theorem-

as we know Z=x+iy is also equal to

This is known as the exponential form of a complex number

De Moivre’s Theorem-

As we know that

this relationship is called De Moivre’s Theorem and this is one of the most important concepts of Mathematics.

This can also be written like this-

$(Cos{\theta _1} + iSin{\theta _1})(Cos{\theta _2} + iSin{\theta _2})......(Cos{\theta _n} + iSin{\theta _n})$ = $Cos({\theta _1} + {\theta _2}......{\theta _n}) + iSin({\theta _1} + {\theta _2}... + {\theta _n})$